遺伝的アルゴリズム×エクセルでリンク機構を設計する

前回の記事では、スプレッドシートで4節リンク機構の設計シートを作ったのに、入力から性能を計算するだけで、その逆（性能から入力を求める）ことができない！という問題が発生したところで終わっていました。

そこで、フェア班の設計者が使っていた、「遺伝的アルゴリズム」なるものを、4節リンクの設計にも使ってみることにしました！

遺伝的アルゴリズムとは、生物の進化の仕組みをまねて、最適な答えを探すアルゴリズムです。遺伝的アルゴリズムに、私の自作設計シートを使わせ、最適な4節リンク機構を設計してもらいます。

具体的には、「遺伝的アルゴリズムが各節点の座標をシートに入力する→設計シートがその入力の際のリンクの性能を計算し出力する→それを遺伝的アルゴリズムが読み取り結果を評価する→評価をもとに遺伝的アルゴリズムが各節点の座標をシートに入力する」といった流れになります。

全部AI任せで、設計シートなんて使わなくていいんじゃないの？と思う方もいるかもしれませんが、あえて、自作の設計シートをAI（遺伝的アルゴリズム）が利用する形にすることで、AIの計算したリンク機構が、設計上本当に優れているのかを確認できます！

プロンプト作成

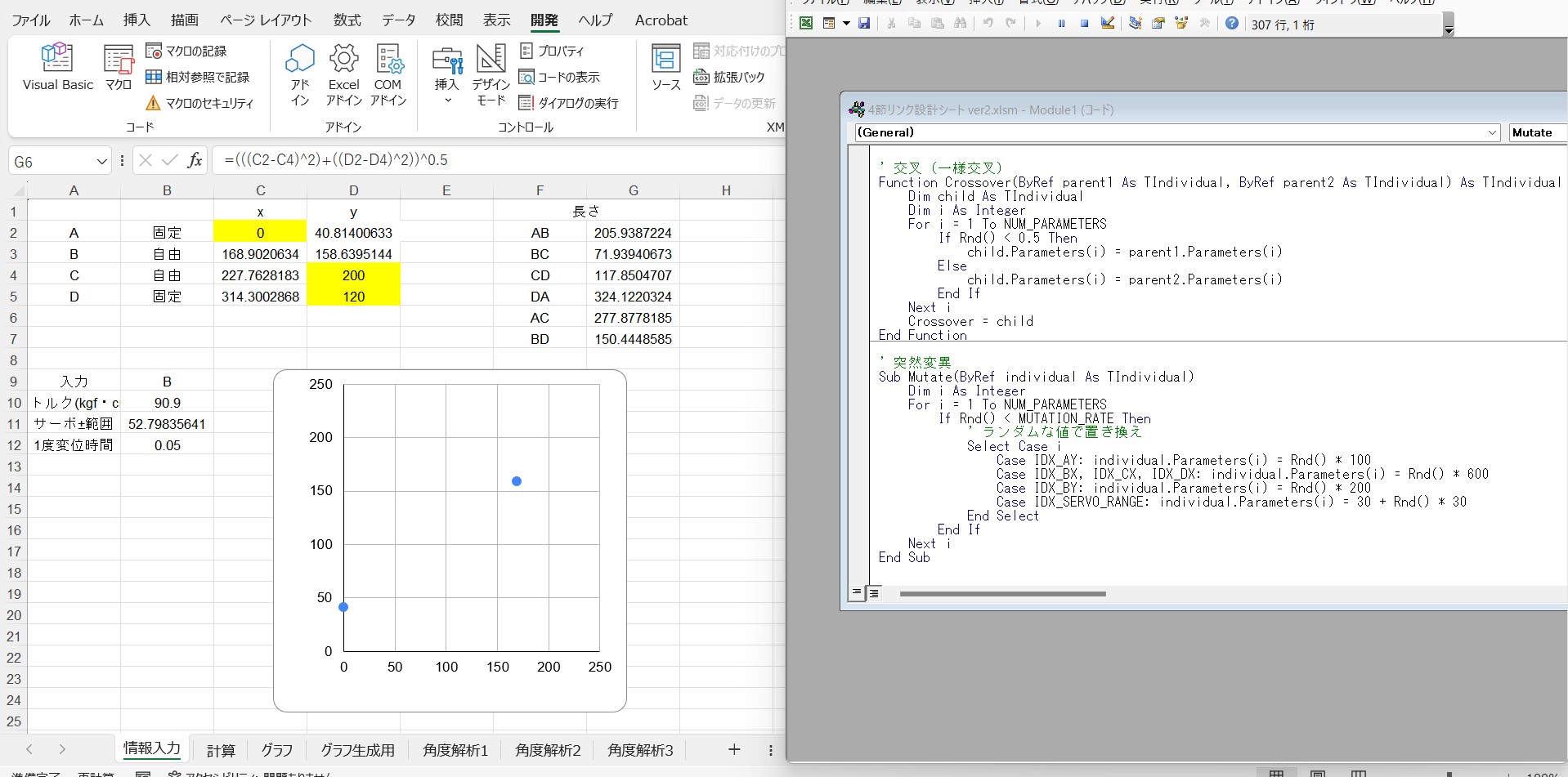
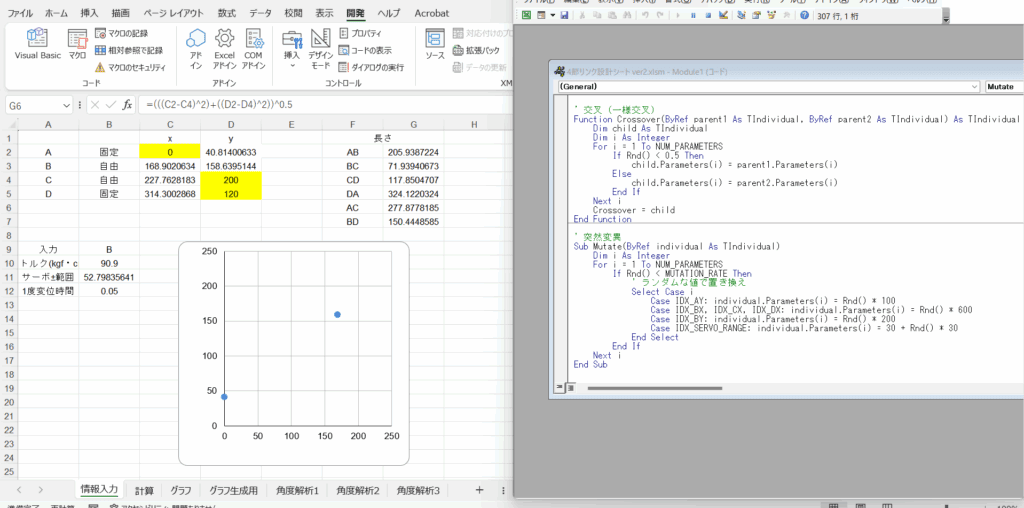
というわけで早速、遺伝的アルゴリズムを作っていきます。GASを用いることで、スプレッドシートをプログラムから編集したり、読み取ったりすることができるので、これを利用します。

プログラムはAIに丸投げするのですが、そのためのプロンプト作成が結構大変でした、、、結局、以下のような滅茶苦茶長いプロンプトで、プログラムを作成してもらいました（最終的には入力角度も計算できるよう更に変更したプロンプトを採用しています）。

飛行機の尾翼を動かす4節リンク機構の設計をするのに、googleスプレッドシートで設計シートを作り、各点の座標や角度や角速度やトルクを計算しています。

4節リンク機構の構成は以下の通りです。
・4つの点ABCDによって構成されています
・Bに入力のサーボがあります
・Dに出力の回転軸があります
・CDに尾翼がついています、ただし、CDがx軸に対し水平のときがニュートラル状態というわけではありません
・DA軸が固定されています
・A軸のx座標が0mm,C軸のy座標が200mm,D軸のy座標が120mmなのは固定で、他のパラメータを調整して設計します
・全ての点について、y座標が負の値をとることはありません
・AがBよりうえ、BがCよりうえに来ることはありません
・ABCについて、Dよりもx座標の値が大きくなることはありません
・サーボの入力（点B）角度は±30度です

設計シートの構成は以下の通りです。
・各点のニュートラル時の座標（入力）
「情報入力」シートのC2セルからD5セルにかけて、各点のニュートラル時の座標を入力します。
C2セル→点Aのx座標
D2セル→点Aのy座標
C3セル→点Bのx座標
D3セル→点Bのy座標
C4セル→点Cのx座標
D4セル→点Cのy座標
C5セル→点Dのx座標
D5セル→点Dのy座標
を入力します。負の値も入力できます。
※このスプレッドシートの長さの単位はmmです
・各節点間の距離（リンクの長さ）（出力）
「情報入力」シートのG2からG7セルにかけて、各節点間の距離（リンクの長さ）が出力されます。
G2セル→AB間の長さ
G3セル→BC間の長さ
G4セル→CD間の長さ
G5セル→DA間の長さ
G6セル→AC間の長さ
G7セル→BD間の長さ

・各節点の角度（出力）
「情報入力」シートのJ2からJ7セルにかけて、各節点の角度（度）が出力されます
J2セル→∠BADの角度
J3セル→∠CBAの角度
J4セル→∠DCBの角度
J5セル→∠ADCの角度
J6セル→∠DAX軸の角度

・サーボの角度をニュートラルから±30度変化させたときの各節点の角度（出力）
「計算」シートのC2セルからF62セルにかけて（-30度から+30度にかけて1度ずつ変化させたとき）、サーボの入力角度の各状態における、各節点の角度が出力されます。
C列→∠BAD
D列→∠CBA
E列→∠DCB
F列→∠ADC
※0度(32行)のとき、「情報入力」シートのJ2からJ5に出力される値と同じになります
・サーボの角度をニュートラルから±30度変化させたときの各節点のニュートラル状態からの角度の変化（出力）
「計算」シートのI2セルからL62セルにかけて（-30度から+30度にかけて1度ずつ変化させたとき）、サーボの入力角度の各状態における、各節点のニュートラル状態からの角度の変化が出力されます。
※0度(32行)のとき、0になります

・サーボの角度をニュートラルから±30度変化させたときの各節点のX,Y座標（出力）
「計算」シートのM2セルからT62セルにかけて（-30度から+30度にかけて1度ずつ変化させたとき）、サーボの入力角度の各状態における、各節点のX,Y座標が出力されます。
M列→点Aのx座標
N列→点Aのy座標
O列→点Bのx座標
P列→点Bのy座標
Q列→点Cのx座標
R列→点Cのy座標
S列→点Dのx座標
T列→点Dのy座標
※0度(32行)のとき、「情報入力」シートのC2からD5に出力される値と同じになります

・サーボの角度をニュートラルから±30度変化させたときの各節点の形成する角度の変化の速度（ここでは角速度と呼びます）（出力）
「計算」シートのU2セルからX61セルにかけて（-30度から+30度にかけて1度ずつ変化させたとき）、サーボの入力角度の各状態における、各節点の角速度が出力されます。
U列→∠A 角速度
V列→∠B 角速度
W列→∠C 角速度
X列→∠D 角速度
※範囲の行が61までのなのは、角度の変化から角速度を求めているため、30度～31度のときの速度が分からないためです

・サーボの角度をニュートラルから±30度変化させたときの各節点の形成する角度の速度の変化の速度（ここでは角加速度と呼びます）（出力）
「計算」シートのY2セルからAB60セルにかけて（-30度から+30度にかけて1度ずつ変化させたとき）、サーボの入力角度の各状態における、各節点の角加速度が出力されます。
Y列→∠A 角加速度
Z列→∠B 角加速度
AA列→∠C 角加速度
AB列→∠D 角加速度
※範囲の行が60までのなのは、角速度の変化から角加速度を求めているため、29度～31度のときの角加速度が分からないためです

・サーボの角度をニュートラルから±30度変化させたときの各節点が回転方向にかけることができるトルク（出力）
「計算」シートのAC2セルからAF61セルにかけて（-30度から+30度にかけて1度ずつ変化させたとき）、サーボの入力角度の各状態における、各節点の回転方向にかけることができるトルクが出力されます。
AC列→点Aのトルク
AD列→点Bのトルク
AE列→点Cのトルク
AF列→点Dのトルク
※サーボ（点A）の入力トルクは事前に定数が与えられており、それに基づいて計算されます
※範囲の行が61セルまでのなのは、角速度を用いてトルク求めているため、30度～31度のときのトルクが分からないためです

この設計シートを用いて設計する4節リンク機構の要件と優先順位は以下の通りです。
・出力（点D）角度は、ニュートラル状態から±10度程度まで動く
・出力のトルクは、どの角度においても最低でも300kgf・cmあり、尾翼がアップの時（Dの角度が大きいとき）のほうが、より、トルクが大きいほうがのぞましい
・入力軸を一定速度で回転させたとき、できるだけ出力軸も一定の角速度で回転する、つまり、点Dの角加速度が0に近い
・点Dのx座標は、最大でも600mm

これから私は、GASを使って、「情報入力」シートの固定されていないパラメータ（D2、C3、D3、C4、C5セル）に様々な値をいれ、各節点の座標として様々な例を試し、上記の条件に沿ったもっともよい結果を得られる座標を知りたいです。遺伝的アルゴリズムを用いて、入力とそれによる出力の結果を何パターンも試し、世代を進化させ、最適な各節点の座標を求めるGASのプログラムを作成してください。つまり、そのGASプログラムを実行すると、自動的にプログラムがシートを用いて最適なリンク機構のための節点の座標を割り出し、ユーザに提示してくれるということです。ただし、シートの計算は重いため、再計算が終わった時点で出力が表示され、次の試行を行えるという点に注意してください。

作ってもらったプログラムをGASに張り付け、実行します。すると、、、動きはしたのですが、、、スプレッドシートって滅茶苦茶重いんですね!?

気を取り直して、エクセルとマクロで再度作ることにしました。

プログラム実行！

そして、実行した様子が以下の動画。遺伝的アルゴリズムが、入力欄に様々な値を入れ、最適な解を探し出そうとしているのがわかるかと思います。

そして算出されたリンク機構がこちら！

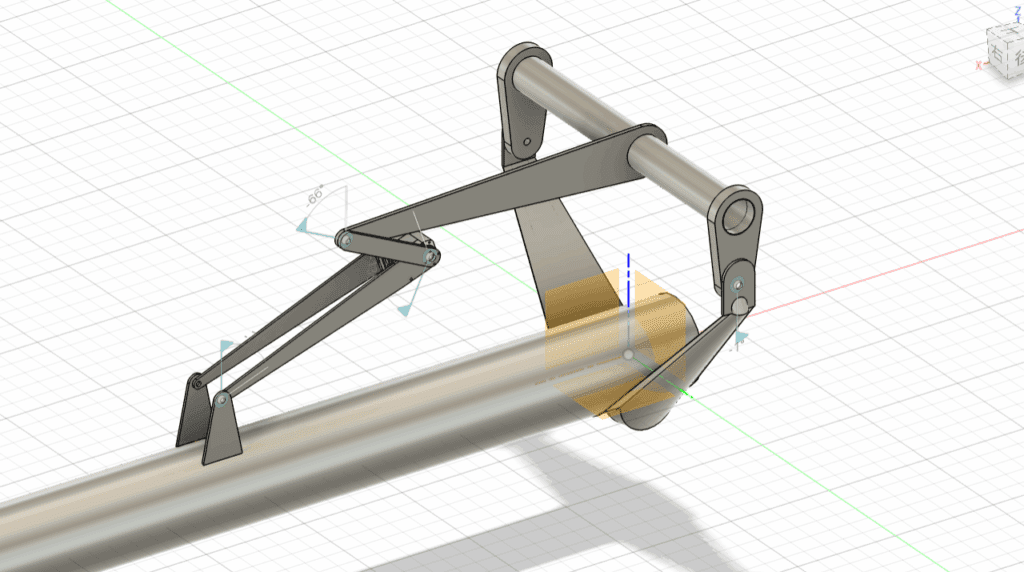
ん、、、？なんか、思ってたのと、、、違う、、、

トルクや角加速度や可動範囲など、様々な要素を考慮して設定してくれたとは思うのですが、どうやら、各項目の点数付け（評価方法）に問題があったらしく、すんごい形になってしまいました、、、（なんかバッタの足みたい）

さらに、舵角を±10度に設定したいのですが、遺伝的アルゴリズムの算出結果が、なかなか言うことを聞いてくれません。

というわけで、アルゴリズムを見直し、評価のパラメータを調整して、再挑戦しようと思います！

また、上記のリンク機構のシミュレーションは、Fusion 360で作成したものなのですが、作っててなかなか面白かったので、次回の記事で詳しく取り上げます！お楽しみに！